填充与步幅
本文基于d2l项目内容整理,介绍卷积神经网络中填充(padding)和步幅(stride)的原理和应用,包括不同填充类型的效果和实现方法。
实践中,习惯使用一致的步幅或填充来控制特征图的尺寸变化。
1. 填充 (Padding)
根据感受野递推公式可知,输入数据经过多个卷积层叠加后,将丢失大量的边界信息。为了使输出特征图的尺寸与输入的保持不变,可在输入数据的边界处填充 (padding) 额外的值以对抗边界信息的丢失。
1.1 填充类型
对于以




根据卷积操作后,输入输出尺寸的变化,填充的类型可分为:
三种填充类型:
有效填充 (Valid Padding):边界处不填充,卷积核只在图像内部滑动
- 输出尺寸 < 输入尺寸
同维填充 (Same Padding):填充边界,使输出与输入尺寸相同
- 输出尺寸 = 输入尺寸
完全填充 (Full Padding):填充更多像素,覆盖整个输入图像
- 输出尺寸 > 输入尺寸
大多数情况,默认使用0填充边界。亦可使用边界处像素的镜像填充边界。
1.2 代码实现
1 | import torch |
2. 步幅 (Stride)
步幅 (stride) 是卷积层中的另一个重要参数,决定了卷积核在输入数据从左上角向右下角每次向下、向右滑动经过的像素数量。
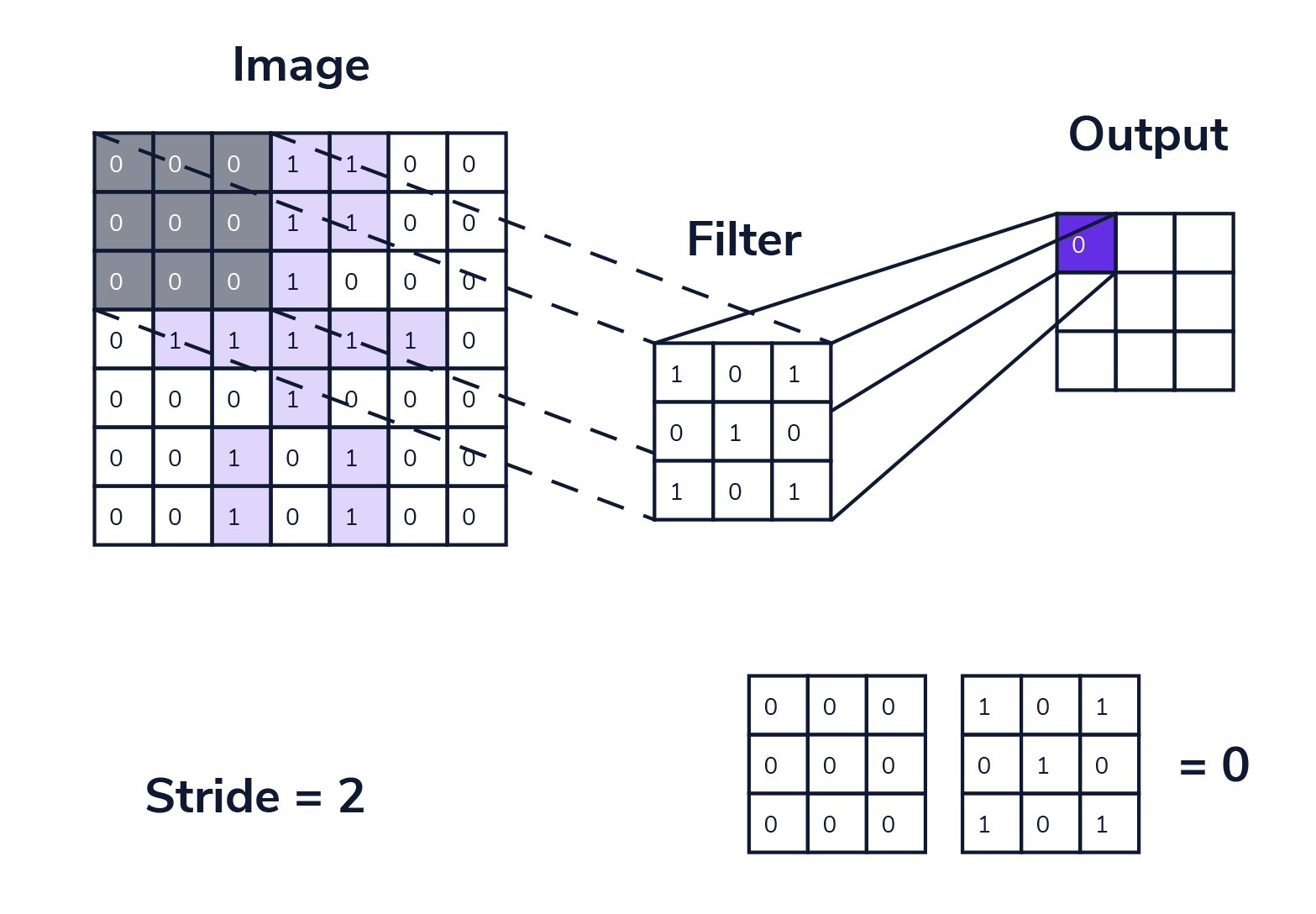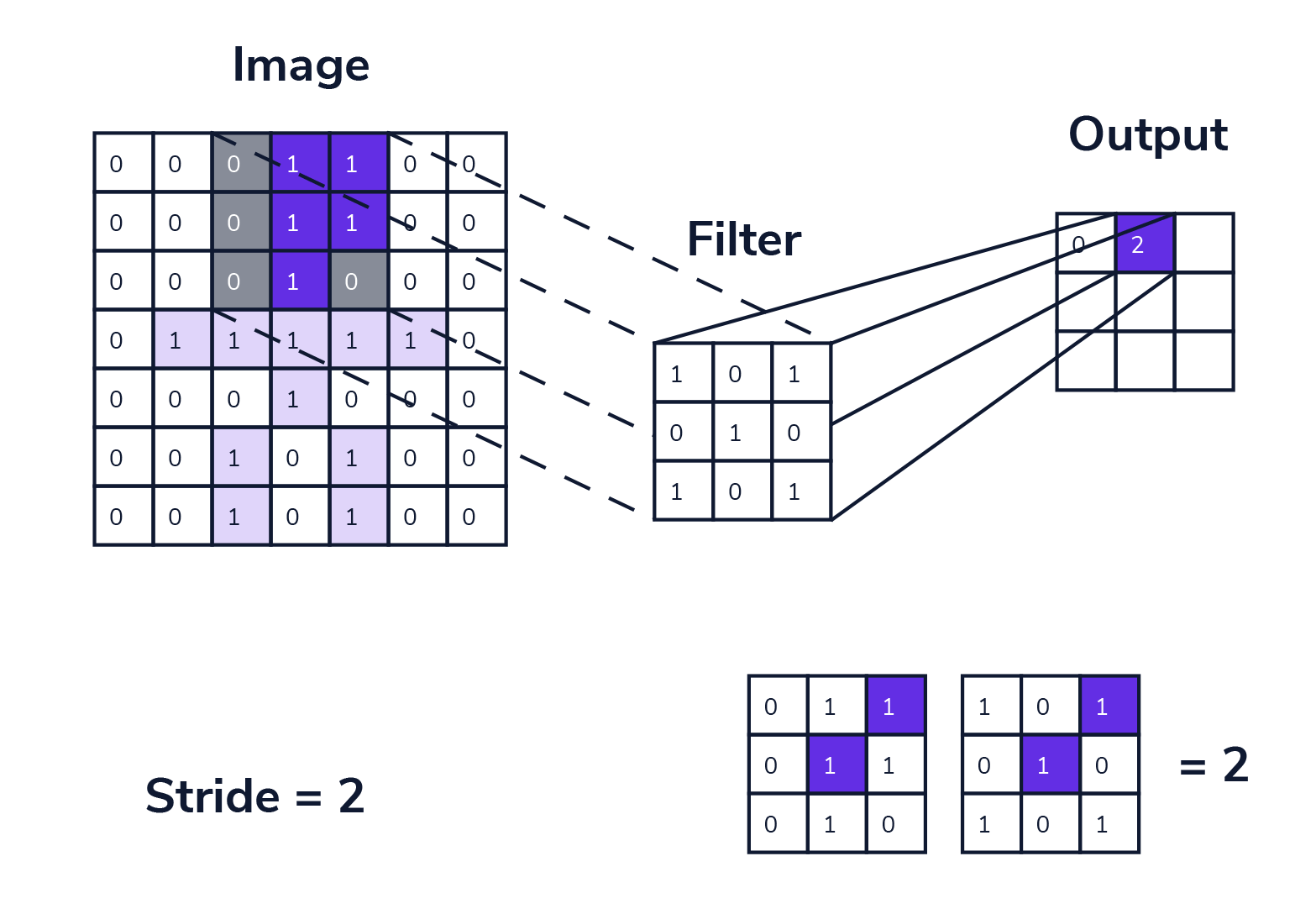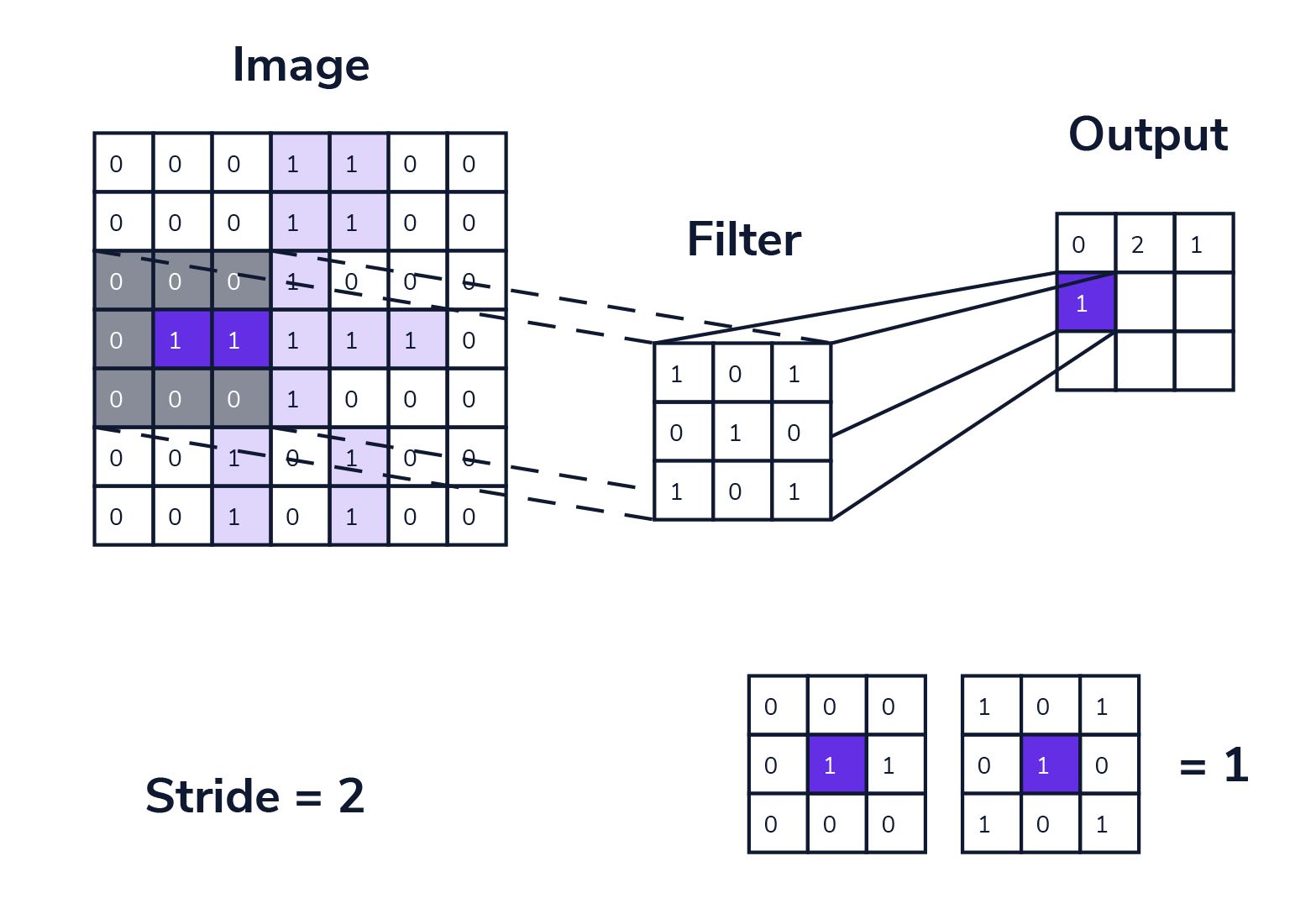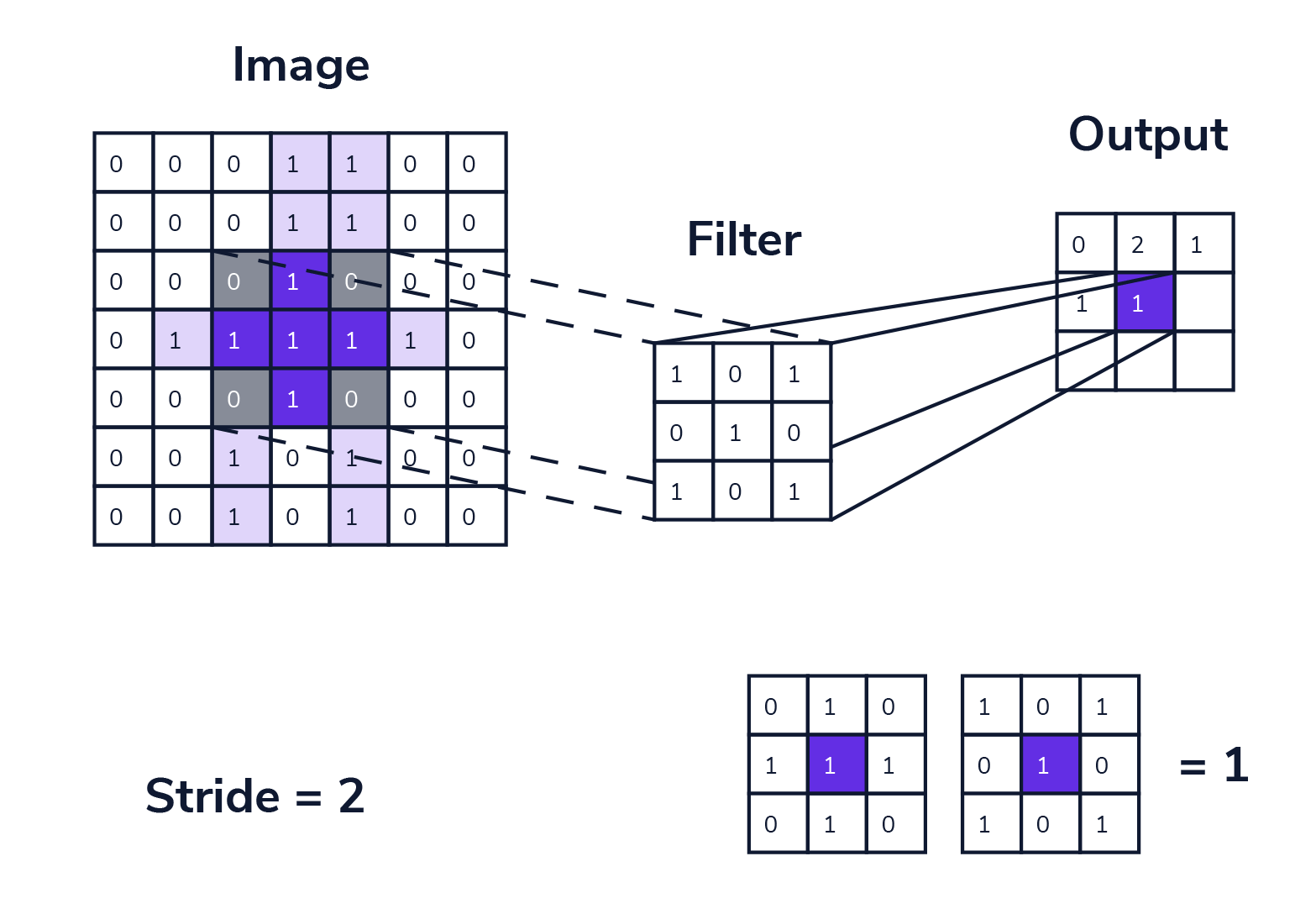
步幅的作用效果:
- 尺寸控制:步幅越大,输出尺寸越小
- 分辨率调节:降低特征图分辨率,提取更高层次特征
- 计算优化:减少计算量和内存消耗
- 去冗余:有助于去除冗余信息,突出重要特征
总结
本文介绍了卷积神经网络中两个关键超参数的作用机制:
📐 填充 (Padding)
- 目的:保持特征图尺寸,防止边界信息丢失
- 类型:有效填充(缩小)、同维填充(不变)、完全填充(扩大)
- 应用:通常使用零填充或镜像填充
🏃 步幅 (Stride)
- 作用:控制卷积核滑动步长,调节输出尺寸
- 效果:步幅越大,输出越小,计算量越少
- 优势:降采样、去冗余、提取高层特征
⚙️ 实际应用
填充和步幅是设计CNN架构的重要工具,通过合理搭配可以:
- 控制网络各层的特征图尺寸变化
- 平衡计算效率和特征表达能力
- 适应不同任务的输入输出需求
评论

