本文基于d2l项目内容整理，介绍多通道卷积操作的原理和实现，包括多通道输入、多通道输出以及1×1卷积层的设计思想和应用场景。

通道 (channel) 的概念：

通道主要用于表示数据的维度，在不同类型的数据中有不同的含义：

  • 图像数据：RGB 图像有红、绿、蓝三种颜色通道，灰度或黑白图像只有一个表示亮度的通道
  • 音频数据：立体声的音频数据有左、右两个声音通道，环绕立体声的音频数据有更多的通道
  • 时序数据：每个传感器单元捕获的数据可分别看作一个通道

在之前的案例中，我们只使用了单通道演示卷积操作，但在实际应用中，更多情况是以 RGB 的色彩模式处理图像数据。因此，我们需要考虑数据维度为 $(c_{in}, h, w)$ 的多通道情况。

1. 多通道输入

多通道卷积的核心原理：

为了分别在各个通道上执行卷积（互相关）操作，当数据以多通道的形式输入时：

  • 通道匹配：卷积核的通道数应与输入数据的通道数一致
  • 结果合并：计算得到 3 维结果，形状为 $(c{in}, h{out}, w_{out})$
  • 特征聚合：将 3 维结果中的每个通道按元素求和，生成单一 2 维特征图

1.1 计算过程

以双通道输入为例：

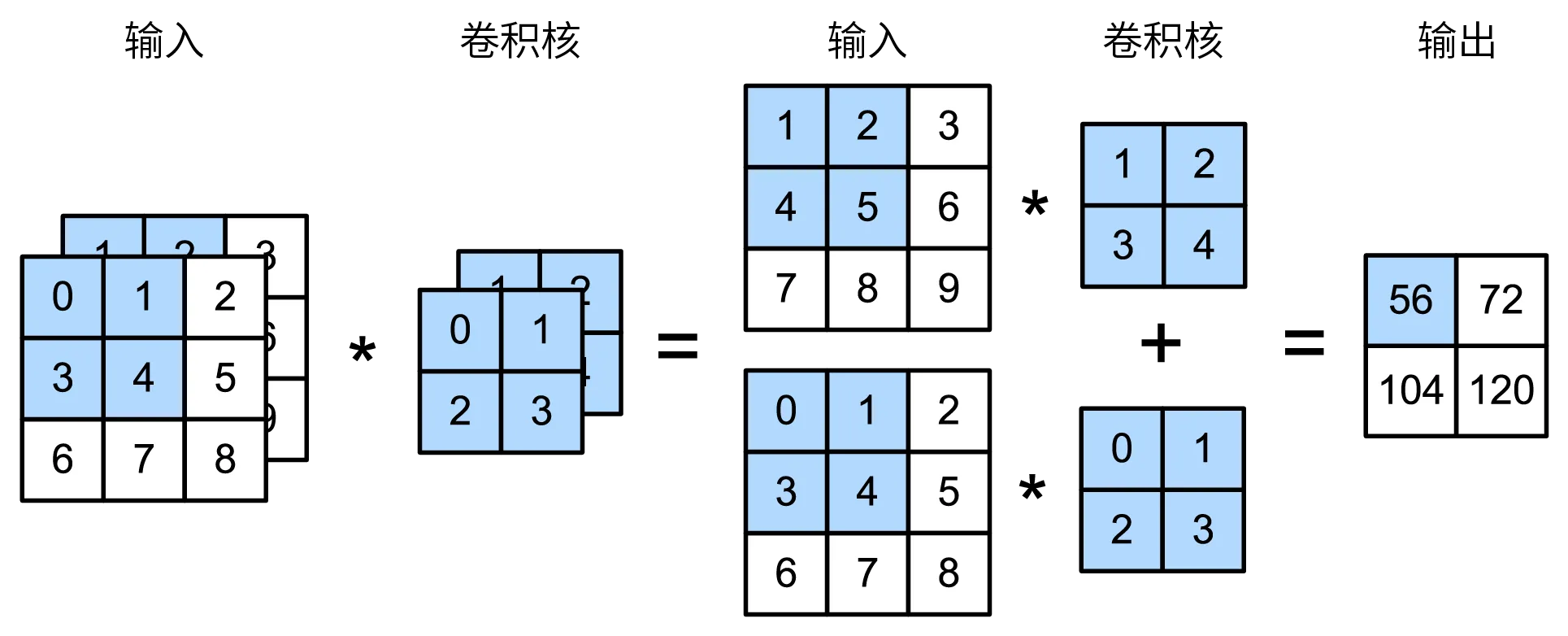
双通道输入的卷积操作示意图
双通道输入的卷积操作示意图

第一个元素的计算详解：

在双通道输入例子中，左上角第一个元素的计算步骤如下：

(1 × 1 + 2 × 2 + 4 × 3 + 5 × 4) + (0 × 0 + 1 × 1 + 3 × 2 + 4 × 3) = 56

1.2 代码实现

下面的实现复用了互相关运算中的 corr2d() 函数来演示多通道卷积：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import torch

def corr2d(X, K):
    """二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

# 双通道输入数据
i = torch.tensor([[[0., 1., 2.],
                   [3., 4., 5.],
                   [6., 7., 8.]],
                  [[1., 2., 3.],
                   [4., 5., 6.],
                   [7., 8., 9.]]])  # (2, 3, 3)

# 双通道卷积核
k = torch.tensor([[[0., 1.],
                   [2., 3.]],
                  [[1., 2.],
                   [3., 4.]]])  # (2, 2, 2)

# 多通道卷积计算
temp = torch.stack([corr2d(c_i, c_k) for c_i, c_k in zip(i, k)])  # 三维中间结果
result = temp.sum(dim=0)  # 二维特征图

print(f'输入形状: {i.shape}')
print(f'卷积核形状: {k.shape}')
print(f'中间结果形状: {temp.shape}')
print(f'最终输出形状: {result.shape}')
print(f'\n输出结果:\n{result}')
查看输出结果 
1
2
3
4
5
6
7
8
输入形状: torch.Size([2, 3, 3])
卷积核形状: torch.Size([2, 2, 2])
中间结果形状: torch.Size([2, 2, 2])
最终输出形状: torch.Size([2, 2])

输出结果:
tensor([[ 56.,  72.],
        [104., 120.]])

2. 多通道输出

多输出通道的设计思想：

可以在卷积层中定义多个卷积核，基于随机的权重初始化，每个卷积核将独立地同时提取不同特征（边缘、纹理）。这样，单个卷积层的输出通道数与卷积核数量相等。

实际上，每个卷积层中的 $c{out}$ 个卷积核（形状为 $(c{in}, kh, k_w)$）以堆栈 (stack) 的方式组织成一个大的卷积核（形状为 $(c{out}, c_{in}, k_h, k_w)$）。

2.1 网络演化规律

CNN网络设计的两个关键趋势：

  • 深度方向：随着网络中卷积层数量的叠加，每层的通道数也往往增加，旨在扩大网络容量以进行更复杂的特征表示
  • 尺寸方向：通过调整步幅和执行池化 (pooling)，每层输出的特征图尺寸（空间分辨率）往往降低，旨在保证计算效率

2.2 协同优化

在网络训练的过程中，卷积层与卷积层之间、卷积层内部各个卷积核之间的参数更新是以整体网络性能的提升而协同优化的。

2.3 代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch

# 双通道输入数据（与之前相同）
i = torch.tensor([[[0., 1., 2.],
                   [3., 4., 5.],
                   [6., 7., 8.]],
                  [[1., 2., 3.],
                   [4., 5., 6.],
                   [7., 8., 9.]]])  # (2, 3, 3)

# 定义三个不同的卷积核
k0 = torch.tensor([[[0., 1.],
                    [2., 3.]],
                   [[1., 2.],
                    [3., 4.]]])  # (2, 2, 2)
k1 = k0 + 1  # 每个元素加1
k2 = k0 + 2  # 每个元素加2

# 将三个卷积核堆叠为多输出通道
k_stack = torch.stack((k0, k1, k2))  # (3, 2, 2, 2)

# 计算多输出通道的卷积
def multi_in_out_corr2d(X, K):
    """多输入多输出卷积"""
    return torch.stack([torch.stack([corr2d(c_x, c_k) for c_x, c_k in zip(X, k)]).sum(dim=0) 
                       for k in K])

result = multi_in_out_corr2d(i, k_stack)

print(f'输出通道数: {result.shape[0]}')
print(f'输出形状: {result.shape}')
print(f'输出结果:\n{result}')
查看输出结果 
1
2
3
4
5
6
7
8
9
10
11
输出通道数: 3
输出形状: torch.Size([3, 2, 2])
输出结果:
tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]])

3. 1×1 卷积层

1×1 卷积层的特殊性：

当卷积层的卷积核尺寸为 1×1 时，该卷积层被称为 1×1 卷积层。这样的卷积层失去了识别宽高维相邻像素间特征的能力，但能继续操作通道，在调整复杂深层网络的通道维度、整合特征和降低计算复杂度等方面非常重要。

以 3 通道输入、2 通道输出的 1×1 卷积层为例：

3通道输入2通道输出的1×1卷积层计算示意图
3通道输入2通道输出的1×1卷积层计算示意图

3.1 1×1 卷积的主要作用

降维与升维

在不改变输出的空间维度前提下，调整卷积核数量改变输出通道数，实现降维与升维。可以在处理较大卷积核时作为”瓶颈层”，减小计算量或提高模型的表达能力。

线性组合通道信息

通过对每个像素位置的通道值加权求和，（与全连接层类似）实现通道间的线性组合。

增加非线性特征的表达能力

与非线性激活函数（如 ReLU）联用后，能增加网络的非线性特征表达能力。

3.2 代码实现

1×1 卷积层可以直接用 torch.nn.Conv2d 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
import torch.nn as nn

# 创建输入数据：(batch_size, channels, height, width)
input_data = torch.randn(1, 3, 32, 32)

# 定义1×1卷积层：3个输入通道 -> 64个输出通道
conv_1x1 = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=1)

# 前向传播
output = conv_1x1(input_data)

print(f'输入形状: {input_data.shape}')
print(f'输入通道数: {input_data.shape[1]}')
print(f'输出形状: {output.shape}')
print(f'输出通道数: {output.shape[1]}')
查看输出结果 
1
2
3
4
输入形状: torch.Size([1, 3, 32, 32])
输入通道数: 3
输出形状: torch.Size([1, 64, 32, 32])
输出通道数: 64

1×1 卷积的优势：

  • 保持空间维度不变：高度和宽度保持 32×32
  • 灵活调整通道数：从 3 个通道扩展到 64 个通道
  • 计算效率高：参数量少，计算复杂度低
  • 增强表达能力：通过通道间的线性组合提取更丰富的特征

总结

本文介绍了多通道卷积操作的核心概念和实现方法：

  1. 多通道输入：卷积核通道数需与输入数据通道数匹配，通过逐通道卷积后求和得到特征图
  2. 多通道输出：使用多个卷积核并行处理，每个卷积核产生一个输出通道
  3. 1×1 卷积：专门用于通道维度的调整和特征组合，是现代CNN架构的重要组件

这些技术为构建深层卷积神经网络提供了基础，使我们能够处理彩色图像等多维度数据，并在保持计算效率的同时提取丰富的特征表示。

[1]
Dive into Deep Learning (D2L)