本文基于d2l项目内容整理，深入讲解图像卷积的数学原理和实现方法，包括互相关运算、边界检测应用以及卷积核的学习过程。

1. 由互相关运算实现的卷积层

1.1 互相关运算

数学上的卷积被定义为，卷积核在水平和垂直方向翻转后，与输入数据滑动求和的过程。而卷积层的设计并没有严格遵循数学上卷积的定义，采用的是其简化形式，没有卷积核翻转的步骤——互相关运算 (cross-correlation)。

以 $I(x,y)$ 为输入，$K(x,y)$ 为卷积核。经典卷积运算 $I*K$ 的定义如下：

$(I*K)(x,y)=\sum_m\sum_nI(m,n)\cdot K(x-m,y-n)$

而互相关运算 $I*K$ 的定义如下：

$(I*K)(x,y)=\sum_m\sum_nI(m,n)\cdot K(x+m,y+n)$

$x-m$ 和 $y-n$ 描述了卷积运算中的翻转后滑动；$x-m$ 和 $y-n$ 描述了互相关运算中未经过翻转的滑动。

只考虑二维的视角。

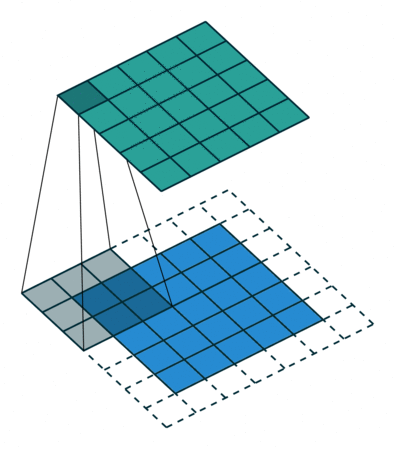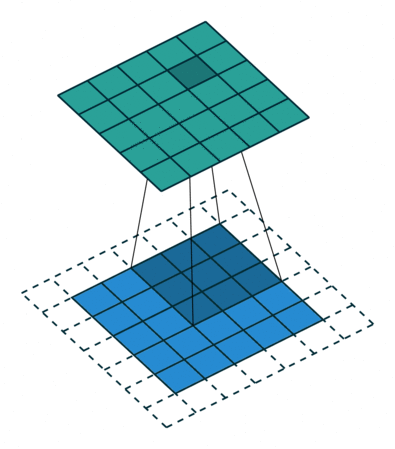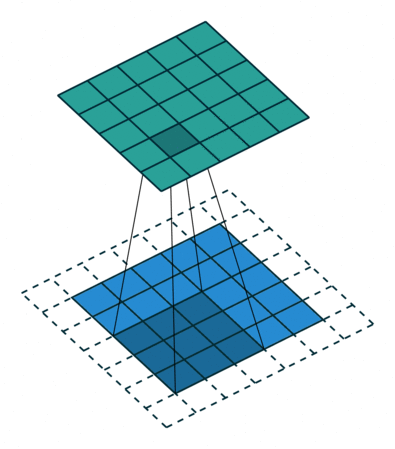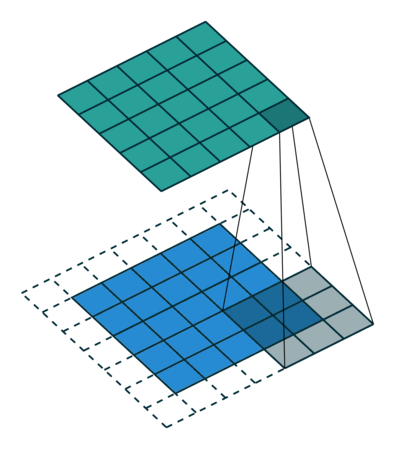
有填充边界的互相关运算保证了输出的大小与输入的大小不变

为什么使用互相关运算？

在卷积层中，用互相关运算替代卷积运算是合理的：

权重视角：卷积核被视为用于更新的权重，翻转权重对特征提取没有助益
计算简化：省去翻转的步骤可简化运算

为了与标准术语保持一致，继续将这种互相关运算称为卷积运算。此外，卷积核上的每个权重被称为元素。

1.2 实现

import torch


def corr2d(input2d: torch.Tensor, kernel: torch.Tensor) -> torch.Tensor:
    """二维的互相关运算"""

    h_input, w_input = input2d.shape
    h_kernel, w_kernel = kernel.shape

    # 不使用填充 (padding) 时的输出尺寸
    h_output = h_input - h_kernel + 1
    w_output = w_input - w_kernel + 1
    output = torch.empty(h_output, w_output)

    # 互相关运算
    for i in range(h_output):  # 遍历输出张量的每一行
        for j in range(w_output):  # 遍历输出张量的每一列
            # 输入的局部区域与卷积核的逐元素相乘，并求和
            output[i, j] = (input2d[i:i + h_kernel, j:j + w_kernel] * kernel).sum()

    return output
if __name__ == '__main__':
    i = torch.tensor([[0.0, 1.0, 2.0],
                      [3.0, 4.0, 5.0],
                      [6.0, 7.0, 8.0]])
    k = torch.tensor([[0.0, 1.0],
                      [2.0, 3.0]])
    o = corr2d(i, k)
    print(o)
tensor([[19., 25.],
        [37., 43.]])

1.3 在边界检测中的应用

图像边缘本质上是图像像素值发生变化的位置，可以用互相关运算检测。

这里给出一个示例：对于一幅像素尺寸为 6×8 的黑白图像，用 1 表示白色，用 0 表示黑色，使用水平差分算子检测水平方向的边缘（亦可选择其他类型的算子检测其他方向的边缘）。

pic = torch.ones(6, 8)
pic[:, 2:6] = 0
k = torch.tensor([[1, -1]])
boundary = corr2d(pic, k)

print(f'{pic.shape = }：\n{pic}')
print(f'{boundary.shape = }：\n{boundary}')
pic.shape = torch.Size([6, 8])：
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])
boundary.shape = torch.Size([6, 7])：
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

输出的结果中，1表示从亮到暗的边缘，-1表示从暗到亮的边缘，0表示非边缘处的像素。

1.4 卷积层

虽然执行的不是经典的卷积运算，但习惯上仍称这个结构为卷积层。

卷积层对输入数据与卷积核（滤波器或权重）执行互相关运算并滑动，添加偏置项后生成特征图 (feature map)（也称为特征映射）。其中，特征图的维数等于卷积层的输出通道数out_channels。卷积核权重的学习过程，就是从输入数据提取边缘、纹理或形状等特征的过程。

在实现卷积层时，与全连接层的实现类似，同样需要定义权重weight和偏置bias 2 个参数：

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) * self.bias

感受野 (Receptive Field)：

神经网络所能”感知”到的输入数据（图像）范围被称为感受野，描述了特征图在输入数据上的”覆盖”区域。感受野的大小决定了网络能捕获的特征大小：

大感受野：可以识别更全局的特征
小感受野：更关注局部细节

可以使用卷积核大小（用表示）、步幅 (stride)、填充 (padding) 及网络的层数，以递推公式的形式量化感受野的大小。第层的感受野为：

其中：

：前一层的感受野；
：第层卷积核的大小；
：第层的步幅。

单卷积层的感受野的大小等于卷积核的尺寸。

以为输入、为卷积核时，步幅为 1 且无填充的单卷积层输出为：

2. 学习卷积核

互相关运算在边界检测中的应用中，直接指定了用于检测水平黑白边缘的卷积核，并很有效。但在更复杂的场景下，希望能“学习到”适合特定模式的卷积核。

于是，在卷积层中将卷积核初始化为随机张量，用深度学习的思想更新卷积核（忽略偏置）：

import torch
from torch import nn

# 卷积层输入数据形状应为 (N, C_in, H_in, W_in)，需要执行 reshape 操作
pic = torch.tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
                    [1., 1., 0., 0., 0., 0., 1., 1.],
                    [1., 1., 0., 0., 0., 0., 1., 1.],
                    [1., 1., 0., 0., 0., 0., 1., 1.],
                    [1., 1., 0., 0., 0., 0., 1., 1.],
                    [1., 1., 0., 0., 0., 0., 1., 1.]]).reshape(1, 1, 6, 8)
boundary = torch.tensor([[0., 1., 0., 0., 0., -1., 0.],
                         [0., 1., 0., 0., 0., -1., 0.],
                         [0., 1., 0., 0., 0., -1., 0.],
                         [0., 1., 0., 0., 0., -1., 0.],
                         [0., 1., 0., 0., 0., -1., 0.],
                         [0., 1., 0., 0., 0., -1., 0.]]).reshape(1, 1, 6, 7)

net = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)  # 单通道输入输出的卷积层，卷积核形状为 (1, 2)
LR = 3e-2
EPOCH = 15

for i in range(EPOCH):
    boundary_hat = net(pic)
    l = ((boundary_hat - boundary) ** 2).sum()
    net.zero_grad()
    l.backward()
    net.weight.data[:] -= LR * net.weight.grad
    print(f'EPOCH: {i + 1:02}/{EPOCH}, LOSS: {l:.3f}')

print(f'\nkernel = {net.weight.data.view(1, 2)}')
EPOCH: 01/15, LOSS: 14.776
EPOCH: 02/15, LOSS: 6.882
EPOCH: 03/15, LOSS: 3.350
EPOCH: 04/15, LOSS: 1.712
EPOCH: 05/15, LOSS: 0.919
EPOCH: 06/15, LOSS: 0.516
EPOCH: 07/15, LOSS: 0.300
EPOCH: 08/15, LOSS: 0.180
EPOCH: 09/15, LOSS: 0.110
EPOCH: 10/15, LOSS: 0.069
EPOCH: 11/15, LOSS: 0.043
EPOCH: 12/15, LOSS: 0.027
EPOCH: 13/15, LOSS: 0.017
EPOCH: 14/15, LOSS: 0.011
EPOCH: 15/15, LOSS: 0.007

kernel = tensor([[ 1.0074, -0.9902]])