权重衰减

本文基于d2l项目内容整理，介绍权重衰减（L2正则化）的数学原理及其在防止过拟合中的应用。

1. 从特征数量限制到权重大小控制

多项式回归的拟合测试让我们感性地意识到：”限制特征的数量“可用于缓解过拟合问题。让我们继续深入这个话题。

1.1 多项式复杂度的组合爆炸

多项式模型的阶数$d$越高，模型的容量也就越大。对于具有$n$个变量的$d$阶多项式，其项数组合可能的个数有：

$$C_{k-1+d}^{k-1}=\frac{(k-1+d)!}{d!\left(k-1\right)!}$$

多项式项数随阶数和变量数的变化

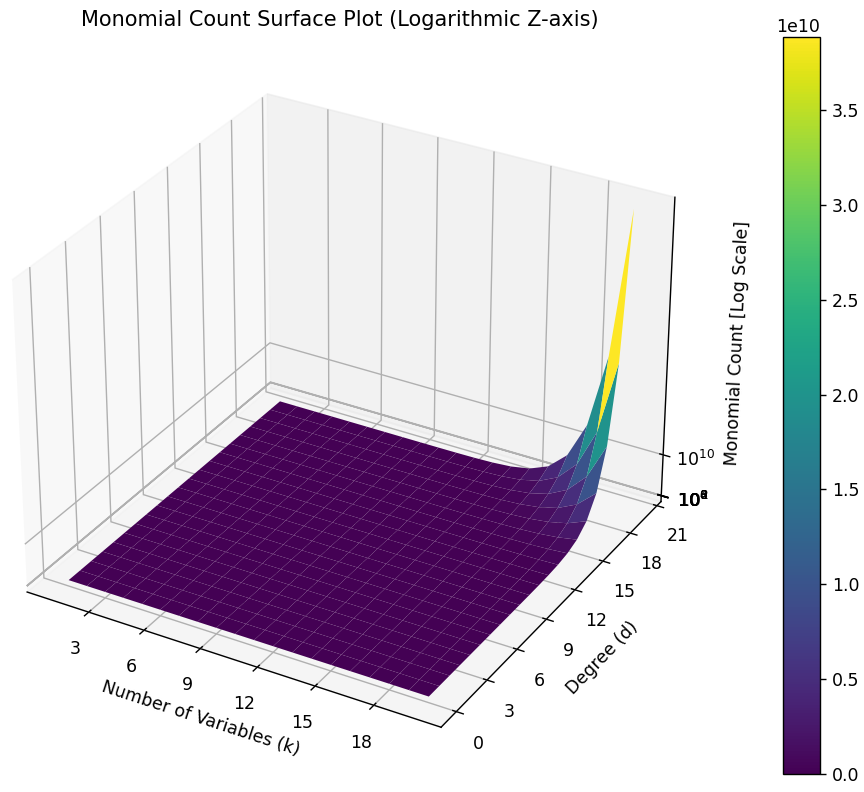
组合爆炸问题：

事实上，仅仅改变阶数（特征的数量），将使模型在简单和复杂间突变。我们需要使用更细粒度的方法调整函数的复杂性，使模型与数据刚好合适。

1.2 权重分布的理想状态

核心思想：

模型的结果不应该过度依赖少数的几个特征，而是大多数特征都具有较小的权重。这样可以提高模型的稳定性和泛化能力。

---

2. 惩罚权重向量的大分量

2.1 范数特性的利用

我们已经知道，$L_2$范数比$L_1$范数更容易受异常值的影响。利用这一特性，为了防止因单个变量具有过高的权重而导致过拟合，我们可以在损失函数中增加一个惩罚项来约束模型的复杂性。

• L2正则化
• L1正则化

L2正则化（权重衰减）

• 别名：Tikhonov正则化、岭回归
• 特点：对权重向量的大分量施加巨大惩罚
• 效果：平滑地减小所有权重，不会产生稀疏解
• 应用：最广泛使用的正则化技术之一

L1正则化（套索回归）

• 特点：$L_1$范数是对模型参数简单性的度量
• 效果：一些特征的权重往往被直接置为零
• 应用：权重集中在一小部分特征上，实现特征选择和稀疏性
• 算法：构成套索回归(lasso regression)算法

2.2 L2正则化的数学表达

以线性回归模型中的损失函数$L$为例，将$L_2$范数作为惩罚项引入后，结合了权重衰减的新损失函数为：

$$\begin{aligned}L_{\mathrm{reg}}&=\frac{1}{2n}\left\|\mathbf{X}\mathbf{w}-\mathbf{y}\right\|_2^2+\frac{\lambda}{2}\|\mathbf{w}\|_2^2\\&=L+\frac{\lambda}{2}\|\mathbf{w}\|_2^2\end{aligned}$$

参数说明

• 损失函数
• 正则化参数

• $L$：原始损失函数
• $L_{reg}$：引入了正则化项的损失函数

• $\lambda$：权重衰减因子，属于超参数（$\frac{1}{2}$是为了简化梯度计算而特意引入的常数因子）
• $|\mathbf{w}|^2$：权重向量$L_2$范数$|\mathbf{w}|_2^2$的平方

L2正则化项的具体形式

对于向量$\mathbf{w} = [w_1, w_2, \ldots, w_d]^T$，$L_2$正则化$|\mathbf{w}|^2$表示为：

$$\|\mathbf{w}\|_2^2=\left(\|\mathbf{w}\|_2\right)^2=\left(\sqrt{w_1^2+w_2^2+\ldots+w_n^2}\right)^2=w_1^2+w_2^2+\ldots+w_n^2=\sum_i^nw_i^2$$

2.3 正则化算法对比

两种主要的正则化算法：

1. 套索回归 (Lasso Regression)：向最小二乘法的损失函数引入$L_1$正则化项

   • 用于产生稀疏解以便特征选择 (feature selection)

2. 岭回归 (Ridge Regression)：向最小二乘法的损失函数引入$L_2$正则化项

   • 用于降低模型复杂性并提高泛化能力

---

3. 权重衰减中的参数更新

3.1 梯度计算

在梯度下降法中（以 Mini-Batch SGD 为例），需要计算$L_{reg}$的梯度。

重要说明：

由于网络输出层的偏置项$b$通常不参与正则化，这里只考虑参数$\mathbf{w}$的更新。

梯度分解

• 原损失函数梯度
• 惩罚项梯度

原损失函数$L$的梯度：

$$\frac{\partial L}{\partial \mathbf{w}}$$

这是不包含正则化项的原始梯度。

惩罚项$\frac{\lambda}{2}|\mathbf{w}|^2$的梯度：

$$\frac{\partial}{\partial \mathbf{w}}\left(\frac{\lambda}{2}\|\mathbf{w}\|^2\right) = \lambda \mathbf{w}$$

这个梯度与权重向量本身成正比。

3.2 参数更新公式

结合两部分梯度，参数更新表示为：

$$\mathbf{w} \leftarrow \mathbf{w} - \eta\left(\frac{\partial L}{\partial \mathbf{w}} + \lambda \mathbf{w}\right)$$

等价变换

我们可以将上式重写为：

$$\mathbf{w} \leftarrow (1 - \eta\lambda)\mathbf{w} - \eta\frac{\partial L}{\partial \mathbf{w}}$$

3.3 收缩因子的作用

收缩因子：

$(1 - \eta\lambda)$被称为收缩因子，用于减小权重值。其中：

• $\eta$：学习率
• $\lambda$：权重衰减系数，用于控制正则化项的强度

权重衰减的直观理解

• 数学角度
• 物理角度
• 实际效果

数学表达：

每次参数更新时，权重都会被乘以一个小于1的因子$(1 - \eta\lambda)$，这导致权重逐渐”衰减”到更小的值。

物理类比：

就像摩擦力会逐渐减慢运动物体的速度一样，权重衰减会逐渐减小模型参数的大小，防止它们变得过大。

实际应用：

• 防止模型过度拟合训练数据
• 提高模型的泛化能力
• 使模型对输入的小变化更加鲁棒

---

4. 权重衰减的实现要点

4.1 超参数选择

权重衰减系数$\lambda$：通常在[$10^{-6}$，$10^{-2}$]范围内选择

学习率$\eta$：需要与权重衰减系数协调选择

验证集调优：通过验证集性能选择最佳的$\lambda$值

4.2 实现注意事项

实现细节：

1. 偏置项处理：通常不对偏置项应用权重衰减
2. 批归一化层：BatchNorm 层的参数通常也不应用权重衰减
3. 不同层的衰减：可以对不同层设置不同的衰减系数
4. 优化器集成：现代深度学习框架通常在优化器中直接支持权重衰减

4.3 与其他正则化技术的结合

权重衰减可以与其他正则化技术结合使用：

• Dropout + 权重衰减
• 数据增强 + 权重衰减
• 早停 + 权重衰减
• 批归一化 + 权重衰减

---

5. PyTorch中的权重衰减实现

5.1 优化器中的权重衰减

在PyTorch中，大多数优化器都支持weight_decay参数：

import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型
model = nn.Linear(10, 1)

# 使用权重衰减的优化器
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)

# 或者使用Adam优化器
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-4)

5.2 手动实现权重衰减

def train_with_weight_decay(model, data_loader, criterion, lr=0.01, weight_decay=1e-4):
    for batch_idx, (data, target) in enumerate(data_loader):
        # 前向传播
        output = model(data)
        loss = criterion(output, target)
        
        # 手动添加L2正则化项
        l2_reg = torch.tensor(0.)
        for param in model.parameters():
            l2_reg += torch.norm(param, p=2)
        
        total_loss = loss + weight_decay * l2_reg
        
        # 反向传播
        total_loss.backward()
        
        # 参数更新
        with torch.no_grad():
            for param in model.parameters():
                param -= lr * param.grad
                param.grad.zero_()

5.3 不同参数组的权重衰减

# 对不同层设置不同的权重衰减
optimizer = optim.Adam([
    {'params': model.conv_layers.parameters(), 'weight_decay': 1e-4},
    {'params': model.fc_layers.parameters(), 'weight_decay': 1e-3},
    {'params': model.bias_params, 'weight_decay': 0}  # 偏置项不使用权重衰减
], lr=0.001)

---

总结

权重衰减（L2正则化）是一种简单而有效的正则化技术：

1. 核心思想：通过惩罚大权重来防止过拟合
2. 数学原理：在损失函数中添加权重的L2范数作为惩罚项
3. 实现方式：在梯度更新中引入收缩因子
4. 实际效果：提高模型泛化能力，增强鲁棒性

权重衰减为我们提供了一种细粒度控制模型复杂度的方法，是深度学习中不可或缺的技术之一。通过合理设置权重衰减系数，我们可以在模型复杂度和泛化能力之间找到最佳平衡点。

[1]

Dive into Deep Learning (D2L)